We determine the Acoustic Thermoplastic behavior by calculating damping factor of the sample polymer material. In addition, we compare the two methods. First, the pulse excitation, and second, the constant wave.
By Shashank Kadagala, Cademix Institute of Technology
The material science community classifies the acoustic thermoplastic materials into four types, based on their individual components. For instance, these are Fibrous materials, perforated panels, granular materials, and polymer foam materials. The industry uses the fibrous materials such as glass, mineral wools, and felts for noise reduction. Most conference rooms, on the other hand, use perforated panels to absorb noise and reduce reflected sound (echo).
To begin, the technical memo serves as an active reference for some of the more commonly used approaches in dynamics analysis. However, there are many ways to calculate the damping factor from data or models. According to the standards, we illustrate the damping factor in two types. First, the half-power method, logarithmic decrement (decay rate) method. Second, a frequency response fitting method. Furthermore, these methods use state-space models and finite element method. For instance, it is very common to use modelling tools like COMSOL Multiphysics (COMSOL), which provides a theoretical damping factor via complex frequency. Each method has its advantages, which we will briefly discuss in the following. In contrast, there are other techniques which we we do not address in this article and we may use them to determine the pulse excitation.

Methodology
Compression of various acoustic thermoplastic damping factors
| Measurement Method | Free Vibration Method | Frequency modulus method |
| Description | The acoustic behaviour of the polymer is calculated by free vibrations | calculation by frequency induced on the sample |
| Source | Pulse Excitation (Physical Pulse) | CW, single frequency, Sine wave generator in the range of 10Hz-10kHz |
| Excitation location | single point | distributed points |
| Main Application Areas | Polymers, Composites | Polymers, Composites |
| Popularity (# of articles published in last 10 years) | 186 Article in the last 10 years | 264 Publication in the last 10 years |
| Boundary Condition / Fixation | One-sided cantilever with a Single degree of freedom. | Free Fall, Multiple degrees of freedom system. |
| Other Requirements | Laser Vibrometer | Laser Vibrometer plus Sound amplifier. |
| Sample Preparation | dogbone and rectangle shape | dogbone and rectangle shape |
| Frequency response | 30 Hz-250 Hz for polymers | Oscilloscope in the spectrum range of 10Hz – 10 kHz with natural peak frequencies until 7kHz for Polymer materials |
| Ease of Implementation | Very easy to implement | Need test setup and time-consuming. |
| Measurement | Measuring reflection and analyzing using a Fourier Transformation | Measuring reflection amplitude |
| Accuracy | Values are accurate in specific frequency | Accurate through frequency bandwidth, |
| Measurement Time | 1 Second for a single measurement | 20-30 Minutes for a complete frequency scan (~30 points) |
| Repeatability | We conduct the test till the sample loses the Elastic properties of the material. | No physical limitation |
Specimens
In this study, we discuss various thermoplastic materials used in the experiment, e.g. acrylonitrile butadiene styrene, polypropylene, and polyamide 6. The samples are attached to the test setup in a cantilever position in one method, while they are free-falling with multiple degrees of freedom in the other, allowing the system to calculate energy loss throughout the process. When compared to the frequency modulus method, the measurement accuracy of the free vibration method is very low. One method is single-point excitation and another method is the average damping factor of multiple points all over the sample. Furthermore, both experiment setups contain a laser vibrometer as a measuring source.

Acoustic behaviour of thermoplastic material
Frequency Modulus Method
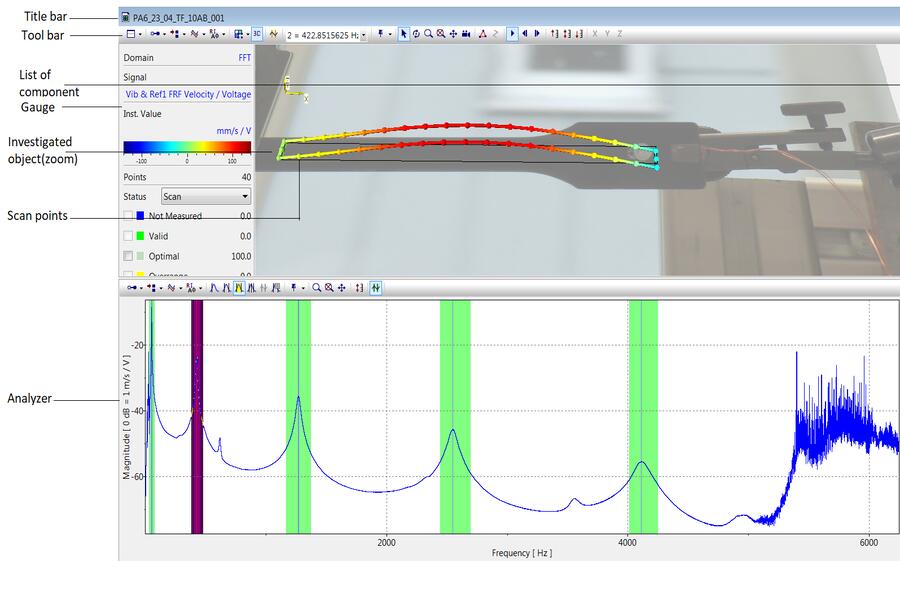
As mentioned in the guidelines, there are specific parameters that must be observed. Therefore, these guidelines specify the amount of time plus excitation required to detect a change in material properties. After that, the Poly-PSV was used to investigate the FEM analysis modifications. The Frequency modulus method consists of devices, such as an amplifier, which boosts the signal to a higher potential and helps the sample stay in motion throughout the experiment. Thus, the sample is in vibration, by inducing an electrical plus at the same time the measurement is calculated. which can be measured using the PSV-500 PSV analysis software will assist us in determining the damping factor over the sample’s surface under normal conditions.
The main motive of the signal generator is to produce a harmonic sine wave over the frequency range (50Hz-10kHz). In another word, we generate an excitation with the help of a sweep generator application. In addition, we can able to generate a continuous sweep over a certain time. However, the application will help us overcome destined accepts like how long a single sweep will be lost for and what is the best frequency to get the sample under vibration. Thirdly, and most importantly PSV analysis software provides us with varieties of options.
We can then choose them according to the working conditions. The trigger time, which determines how long each trigger should be lost and how long the vibrometer has to scan each point, is one of the most important parameters. In conclusion, the laser vibrometer helps us to calculate the energy loss after that It will tell us the acoustic behaviour of the thermoplastic material.
Frequency Analysis
The following Figure shows the Frequency modes of the sample with FEM analysis. Green intervals indicates the Full Width Half Max (FWHM) for each resonance peak. Subsequently, these can be used to calculate the Quality factor according to the formula Q = Omega / FWHM, where Omega is the angular frequency.
Results and Conclusion
To conclude, we investigated the acoustic behaviour of two composite materials. First, the normal composite material. Second, the material with water content. Moreover, we improved test method for obtaining successful inner damping values at higher frequencies and how they affect the material’s structure. Further, the article demonstrates the parameters that influence the acoustic behaviour of fibre-reinforced polymer materials with various geometries.
Thermoplastic materials are used in a variety of applications, such as modern automobiles, sound systems, and audio amplifiers. The initial setup is therefore not for complex materials like poly-amid 6 conditions. In contrast, this material has water content from (0-7,39%) as the material has an almost similar microscopic structure with a slight change in weight and composition. Hence, the data from the Free-vibration method demonstrates the variation in the damping factor. As a result, we proceed with the Frequency model analysis in order to obtain accurate values.
Related Keywords
Moreover, we use a few important keywords Introduction to Polymer, engineers, Interdisciplinary, To design, Problem-solving, Cad, Three-dimensional, Mechanical engineering, Aerospace, Acoustic, Numerical, Aided design, Engineering technology, Computer-aided design. In addition, other keywords are Design process, Composite materials, Fibre-reinforced, Mechanical test, Injection moulding, Manufacturing, FEM analysis, advance Excel programming, Laser, laser Doppler vibrometer, Plus excitation, electrical, sound wave, Sinewave, White noise, audio amplifier.

